Kvantumszámítógép

A kvantumszámítógép olyan számítóeszköz, amelyik úgy végez számításokat, hogy kvantummechanikai jelenségeket használ, mint a kvantum-szuperpozíció és a kvantum-összefonódás.

Egy kvantumszámítógép képes lehet olyan számítások hatékony végzésére, amik a hagyományos, digitális számítógépekkel gyakorlatilag megoldhatatlanok. Kutatását és későbbi megvalósítását elsősorban kormányszervek támogatják. A kvantumszámítógép gyakorlati megvalósítása a kezdeti lépéseknél tart, egyelőre kísérleti fázisban van.

A kvantumszámítógép a számításokat egymással párhuzamosan hajtja végre, ezért programozásához speciális programozási módszer szükséges.

A kvantummechanikai hatások miatt a rendszert közel abszolút nulla fokra kell folyamatosan hűteni. Vezetékezése koaxiális kábelekkel történik, amik szupravezető tulajdonságúak (ezek szintén igen alacsony hőmérsékleten működnek). A bemenetet mikrohullámú impulzusok jelentik, amik befolyásolják a részecskék állapotait. A kimenő jeleket magas szintű kvantummechanikai ismeretekkel rendelkező operátorok értelmezik. 2018-ban az IBM és a Rigetti nevű cég fejlesztői azon dolgoznak, hogy az értelmezés könnyebbé váljon.

Hagyományos számítógép

A hagyományos számítógépben az információt bitekben tárolják, melynek két lehetséges értéke van: 0 (hamis) vagy 1 (igaz).

A hagyományos számítógép hardvere erősnek mondható, ezért rengeteg számítást tud elvégezni másodpercek alatt. Azonban gyengeségei közé tartoznak az alábbi területek: képfelismerés, természetes nyelvek, gépi tanulás és az optimalizációs problémák.

A kvantumszámítás története

• 1980: Paul Benioff fizikus azt javasolja, hogy a kvantummechanikát számításokra lehetne használni.
• 1981: Richard Feynman Nobel-díjas fizikus megalkotja a kvantumszámítógép kifejezést.
• 1985: David Deutsch fizikus (Oxford) leírja, hogyan működne egy kvantumszámítógép.
• 1994: Peter Shor matematikus (Bell Labs) olyan algoritmust ír, ami fel tudja törni a napjainkban széles körben használt titkosítási eljárásokat.
• 2007: A D-wave nevű kanadai startup cég bejelenti, hogy kvantumszámítással működő integrált áramköre képes megoldani szúdokufeladatokat.
• 2012: A Google létrehozta a Quantum Artificial Intelligence Laboratory-t, amelyet a NASA-val, hogy teszteljék a D-wave hardverét.
• 2017: A Rigetti nevű startup cég gyártóüzemet nyit kvantumszámítógép hardverének gyártására.
• 2019: A Google kutatói azt állították, elérték a kvantumfölény. Az áttörésről szóló tanulmány a Nature tudományos folyóiratban jelent meg.
• 2024: a Google bejelentette, hogy a Willow kvantumchipet használó kvantumszámítógépe olyan feladatot oldott meg percek alatt, amely a világ akkori legerősebb szuperszámítógépének több milliárd évig tartott volna.

A kvantumszámítás alapelvei

• Egy kvantumszámítógép kvantumbitek sorozatát kezeli.
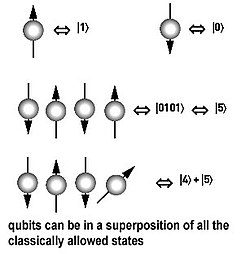
• Egy kvantumbit nullát, egyet vagy ezek kvantum-szuperpozícióját tartalmazhatja, ami végtelen számú állapotot tesz lehetővé. Egy kvantumszámítógép ezeket a kvantumbiteket kvantum logikai kapuk használatával manipulálja.

Egy kvantumszámítógéphez a kvantumbitek egy lehetséges megvalósítása indulhat például két spinállapotú részecske használatával. Valójában azonban bármely A megfigyelhető mennyiség megfelelő jelölt lehet kvantumbitek megvalósítására, amelyik az idő múlásával megmarad, továbbá A-nak van legalább két, diszkrét és jól megkülönböztethető sajátértéke.

A kvantumbitek kezelése

A kvantumbiteket mikroszkopikus részecskék testesítik meg. Ezek kezeléséhez vezérlőeszközök szükségesek, amik például az alábbiak lehetnek:

• Ioncsapda: optikai vagy mágneses teret alkalmaz (vagy ezek kombinációját), amivel ionokat tud irányítani
• Optikai csapda: fényhullámokat alkalmaz
• Félvezető anyag, ami elektronokat tartalmaz és befolyásol
• Szupravezető áramkör: az elektronok szinte elektromos ellenállás nélkül haladnak benne alacsony hőmérsékleten

• Fémként viselkedő szén nanogömbök
• Speciális tranzisztorok
• Ritkaföldfém-ionokkal szennyezett szervetlen kristályok

Bitek és kvantumbitek

Tekintsünk egy klasszikus számítógépet, amelyik egy 3 bites regisztert kezel. A regiszter bitjei minden időpillanatban meghatározott állapotban vannak, mint például 101.

Egy kvantumszámítógépben a kvantumbiteket a klasszikusan megengedett állapotok szuperpozíciójával adhatjuk meg. A regisztert egy hullámfüggvény írja le:

$|\psi ⟩=a|000⟩+b|001⟩+c|010⟩+d|011⟩+e|100⟩+f|101⟩+g|110⟩+h|111⟩$

A kvantumbitek kontrollált részecskékből és vezérlőeszközből állnak (például a részecskéket csapdában tartó eszköz, amelyik azokat egyik állapotból a másikba kapcsolja).

ahol az a, b, c,…, h együtthatók komplex számok, amelyeknek amplitúdónégyzete annak valószínűségét adja meg, hogy a méréssel a kvantumbitet az egyes állapotokba tartozónak mérjük. Például, $|c{|}^2$ annak valószínűsége, hogy a regisztert a 010 állapotban találjuk. Mivel ezek komplex számok, a számok hullámfázisai egymással konstruktív vagy destruktív módon interferálnak; ez a kvantumalgoritmusok fontos tulajdonsága.

Egy kvantumregiszter leírásához exponenciálisan növekvő számú komplex szám szükséges (a fenti 3-kvantumbites regiszter leírásához $2^3=8$ komplex szám szükséges). A valamely kvantumállapot becslésére szükséges klasszikus bitek száma a kvantumbitek számával exponenciálisan nő. Egy 300 kvantumbites kvantumregiszterhez 10⁹⁰ (2³⁰⁰) nagyságrendű klasszikus regiszter szükséges, ami több, mint ahány atom van a megfigyelhető világegyetemben

Kezdőértékadás, végrehajtás és kilépés

Példánkban a kvantumbit regiszterek tartalmát 8 dimenziós komplex vektornak tekinthetjük. Egy kvantum számítógép algoritmusnak ezt a vektort meghatározott módon el kell látnia kezdőértékkel. Ezt a vektort az algoritmus minden egyes lépésében úgy kell módosítani, hogy megszorozzuk egy unitér mátrixszal. A mátrixot az eszköz fizikai felépítése határozza meg. A mátrix unitér volta biztosítja, hogy a mátrix invertálható, azaz minden egyes lépés visszafordítható.

Az algoritmus befejeződése után a regiszterben tárolt 8 dimenziós komplex vektort valamiféle kvantumos méréssel ki kell olvasnunk a kvantumbit regiszterből. A kvantummechanika törvényei szerint azonban ennek a mérésnek az eredménye egy 3 bites véletlen string lesz (és ráadásul a tárolt állapot is megsemmisül). Ezt a véletlen bitstringet használhatjuk egy függvényérték kiszámítására, mivel (az alapelvből következően) a mért kimenő bitstring valószínűségi eloszlásának nagyobb értékei a függvény helyes értéke körül csúcsosodnak. A kvantumszámítógép ismételt futtatásával és a kimenet ismételt megmérésével meghatározhatjuk a nagy valószínűséggel helyes eredményt, olyan módon, hogy a lekérdezett kimeneti eredmények közül a gyakoribbat fogadjuk el. (Azaz, a klasszikus, 'nulla' és 'egy' állapotokon alapuló elektronikus számítógépektől eltérően, a kvantumos számítások kvantumbiteken alapulnak, amelyek a 'nulla' és 'egy' mellett valószínűségi alapú kvantum szuperpozíciós állapotot is jelentenek.) Röviden, a kvantumos számítások valószínűségi jellegűek.

A különböző algoritmusokban használt műveleteket illetően a részletekért lásd a következő szócikkeket:

• Shor-algoritmus
• Grover-algoritmus

A kvantumszámítógépek teljesítménye

Kvantumszámítógéppel polinomiális időben megoldható problémaosztály (angol rövidítése BQP) feltételezhető besorolása a bonyolultságelméleti problémaosztályok közé

Az egész számok faktorizációja olyan feladat, amelyről azt hisszük, hogy a hagyományos számítógépekkel megoldhatatlan, legalábbis olyan nagy egész számok esetén, amelyek csak néhány prímszám szorzatából állnak (például két 300-jegyű prímszám szorzata). Összehasonlításul, egy kvantumszámítógép a törzstényezőkre bontás problémáját a Shor-algoritmus használatával sokkal hatékonyabban tudná megoldani, mint egy klasszikus számítógép. Ez a képesség lehetővé tenné, hogy egy kvantumszámítógép "feltörje" a ma használatos kriptográfiai rendszerek sokaságát, abban az értelemben, hogy (az egész szám bitjeinek száma szerint) polinomiális idő alatt megoldaná a feladatot. Nevezetesen, a legnépszerűbb nyilvános kulcsú kódok, beleértve az RSA-t, azon alapulnak, hogy nehéz az egészeket faktorizálni. Ezeket használjuk biztonságos weboldalak, titkosított e-mailek és számos más adattípus védelmére; feltörésük szörnyű következményekkel járna az elektronikus magánszféra és titkosítás számára.

Az egyetlen lehetőség az RSA-szerű algoritmusok biztonságának növelésére az lenne, hogy megnöveljük a kulcs méretét és reménykedünk abban, hogy az ellenfélnek nincs elég erőforrása arra, hogy kellően teljesítőképes kvantumszámítógépet építsen és használjon.

A problémából kivezető út valamiféle kvantumkriptográfia használata lehet. Vannak olyan digitális aláírás (digital signature) sémák, amelyekről azt hisszük, hogy védettek a kvantumszámítógépek ellen; lásd például a Lamport aláírást.

A kvantumszámítógépek előnyét 2008-ban csak a következő problémákra találták ilyen drámainak: faktorizáció és diszkrét logaritmus. Nincs azonban bizonyíték arra sem, hogy ez az előny valódi: még felfedezhetnek egy hasonlóképpen gyors klasszikus algoritmust. Van még egy probléma, ahol a kvantumszámítógépeknek kisebb, de azért jelentős (kvadratikus) előnye van. Ez a kvantumos adatbázis keresés, és a Grover algoritmussal oldható meg. Ebben az esetben be is bizonyítható az előny. Ez minden kétséget kizáróan bizonyítja, hogy a(z ideális) kvantumszámítógépek legalább egy probléma esetén jobbak a hagyományos számítógépeknél.

Tekintsünk egy olyan problémát, amelyik rendelkezik az alábbi négy tulajdonsággal:

1. A megoldás egyetlen módja, hogy ismételten megpróbáljuk kitalálni a válaszokat, és megvizsgáljuk őket.
2. Összesen n megvizsgálandó válasz van.
3. Minden egyes lehetséges válasz megvizsgálása ugyanannyi időt vesz igénybe.
4. Fogalmunk sincs róla, melyik lehet jobb válasz: a lehetőségeket véletlenszerűen generálni épp olyan jó, mint egy speciális sorrendet használni.

Ennek egy példája egy jelszótörő, ami a jelszót egy kódolt fájl alapján próbálja kitalálni (feltéve, hogy a jelszónak van maximális hossza).

A mind a négy tulajdonsággal rendelkező problémák esetén egy kvantumszámítógép számára szükséges megoldási idő n négyzetgyökével lesz arányos (egy klasszikus számítógépnek (n + 1)/2 próbálkozás szükséges a válasz megtalálásához). Ez nagyon nagy gyorsulás is lehet, ami bizonyos problémák megoldásának idejét évekről másodpercekre csökkentheti. Ezt már arra is használhatnánk, hogy eséllyel próbáljuk meg a szimmetrikus kódolású eljárások (mint a tripla DES és AES titkos kulcsát kitalálni. Függetlenül attól, hogy ki tudjuk-e mutatni, hogy ezen problémák megoldására előnyösebb kvantumszámítógépet használni, ez mindenképpen kitűnő segédeszköz kvantummechanikai kölcsönhatások tanulmányozására, ami önmagában is hatalmas érték a tudományos közösség számára.

Problémák és eredmények

Egy kvantumszámítógép építésekor számos gyakorlati nehézség fordul elő, így eddig kvantumszámítógéppel csak triviális problémákat oldottak meg. David DiVincenzo (IBM) a következő követelményeket fogalmazta meg a gyakorlatban is használható kvantumszámítógéppel szemben:

• a kvantumbitek növelése érdekében fizikailag skálázható
• a kvantumbitek tetszőleges kezdőértékre beállíthatók
• a kvantumkapuk gyorsabbak, mint a dekoherencia ideje
• van univerzális kapu készlete
• a kvantumbitek könnyen kiolvashatók

Mérnöki szemmel nézve egy olyan rendszert kell létrehozni, amelyik el van szigetelve mindentől, kivéve a mérő és vezérlő mechanizmusokat. Ezen túlmenően, képesnek kell lennünk arra, hogy kikapcsoljuk a kvantumbitek és a mérés közötti csatolást, hogy ne oltsuk ki a kvantumbiteket, miközben műveleteket végzünk velük.

2012-ben Hartmut Neven alapította meg a Google-ön belül a Quantum Artificial Intelligence Laboratory-t, amely a NASA-val és más kutatóintézetekkel együttműködve a kvantumszámítástechnika és a mesterséges intelligencia (MI) fejlesztését tűzte célul maga elé. A kvantumszámítógépek fejlesztése terén fontos előrelépést jelentett a 2019 októberében elkészített kvantumszámítógépük, mely vákuumos, −273 °C alatti kamrában, 53 kvantumbittel működott. Sikeresen demonstrálták a kvantumfölényt a Sycamore processzor segítségével, amely egy olyan számítást végzett el, amely a leggyorsabb klasszikus szuperszámítógépek számára 10 000 évig tartott volna.

2024 decemberében Hartmut Neven bejelentette, hogy a Quantum Artificial Intelligence Laboratory Willow kvantumchipet használó kvantumszámítógépe olyan feladatot oldott meg percek alatt, amely a világ akkori legerősebb szuperszámítógépének több milliárd évig tartott volna. A Google kvantumszámítógépe egy összehasonlító algoritmus futtatásában múlta felül a Frontier szuperszámítógépet. A feladat megoldása a Google új gépének 5 percet vett igénybe, míg a Frontiernek 10 szeptilliárd évre lett volna szüksége a feladvány megoldásához. (1 szeptillárd év 10,000,000,000,000,000,000,000,000 évet jelent.) Ugyanakkor a kvantumszámítógépek működéséhez elengedhetetlen rendkívül alacsony, 0 K (kelvin) körüli hőmérséklet megteremtésének igénye óriási mértékben megnehezíti a technológia gyakorlati alkalmazását és méretezhetőségét.

Források

• The Wired Guide to Quantum Computing, 2018-08-22
• howstuffworks: How Quantum Computers Work

Külső hivatkozások

• DiVincenzo, David P. (2000). "A kvantumos számítások fizikai magvalósítása". Experimental Proposals for Quantum Computation.
• Sablon:Cite journal Az 1. táblázat felsorolja a különféle rendszerek kapcsolási és fázisfosztási időit.
• Sablon:Cite journal
• Sablon:Cite book"
• Sablon:Cite book
• Sablon:Cite book
• Sablon:Cite book
• http://jquantum.sourceforge.net/jQuantumApplet.html Kvantumszámítógép szimulátor (Java applet).
• reality of quantum computing could be just three years away, 2018-09-07