Klikkszélesség

Egy 3 klikkszélességű távolság-örökletes gráf konstrukciója diszjunkt uniókkal, átcímkézésekkel és címke-egyesítésekkel. A címkéket az ábrán színek jelzik.

A matematika, azon belül a gráfelmélet területén egy gráf klikkszélessége (clique-width) a gráf szerkezetének bonyolultságát leíró paraméter; közeli rokona a faszélességnek, de attól eltérő módon, sűrű gráfokon is korlátos lehet az értéke. A definíció szerint értéke megegyezik a $G$ gráf konstruálásához szükséges címkék minimális számával, ha a következő négy művelet engedélyezett:

1. Felveszünk egy új csúcsot, v-t és i címkével látjuk el (jelölés: i(v) vagy ${\bullet }_i$)
2. Két címkézett gráf, G és H diszjunkt unióját képezzük (jelölés: $G\oplus H$)
3. Minden i-vel jelölt csúcsot összekötünk minden j-vel jelölt csúccsal (jelölés: η(i,j)), ahol $i\ne j$
4. Átnevezzük az i címkét j-re (jelölés: ρ(i,j) )

A korlátos klikkszélességű gráfok közé tartoznak a kográfok és a távolság-örökletes gráfok is. Bár általános esetben a klikkszélesség meghatározása NP-nehéz feladat, és nem tudjuk, vajon polinom időben kiszámítható-e abban az esetben, ha korlátos, ismert több hatékony közelítő algoritmus a klikkszélesség kiszámítására. Ezekre az algoritmusokra és a Courcelle-tételre alapozva számos, általános gráfokon NP-nehéz gráfoptimalizálási probléma gyorsan megoldható vagy közelíthető a korlátos klikkszélességű gráfokon.

A klikkszélesség fogalmához szükséges konstrukciós lépéseket Courcelle, Engelfriet és Rozenberg fogalmazta meg 1990-ben Sablon:Sfnp, majd Sablon:Harvtxt. A „klikkszélesség” kifejezést először Sablon:Harvtxt használta egy másik fogalom leírására, de 1993-ra már a jelenlegi értelemben használták.Sablon:Sfnp

Példa

A $C_6$ konstrukciós lépéseinek kifejezés-fája

A 6 csúcsból álló $C_6$ gráf klikkszélessége nem nagyobb 3-nál, mivel a következő műveletek segítségével előállítható:

Klikkszélesség-művelet	A gráf vizualizációja
$G_1={\bullet }_1$
$G_2={\bullet }_2$
$G_3=G_1\oplus G_2$
$G_4={\eta }_{1,2}(G_3)$
$G_5=G_4\oplus G_4$
$G_6=G_5\oplus {\bullet }_3$
$G_7={\eta }_{1,3}(G_6)$
$G_8={\rho }_{3\to 1}(G_7)$
$G_9=G_8\oplus {\bullet }_3$
$C_6={\eta }_{2,3}(G_9)$

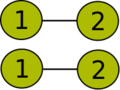
Az előállított $3$-művelet a következő:

$X={\eta }_{2,3}({\rho }_{3\to 1}({\eta }_{1,3}(\eta ({\bullet }_1\oplus {\bullet }_2)\oplus \eta ({\bullet }_1\oplus {\bullet }_2)\oplus {\bullet }_3))\oplus {\bullet }_3)$

A jobb oldalon látható az $X$ 3-kifejezés fája.

Speciális gráfosztályok

A kográfok megegyeznek azokkal a gráfokkal, melyek klikkszélessége legfeljebb 2.Sablon:Sfnp A távolság-örökletes gráfok klikkszélessége legfeljebb 3. Az egység-intervallumgráfok klikkszélessége azonban (rácsos szerkezetük miatt) korlátlan.Sablon:Sfnp Hasonlóan, a páros permutációgráfok klikkszélessége (hasonlóan a rácsos szerkezet maitt) korlátlan.Sablon:Sfnp A kográfok egyik karakterizálása szerint ezek a gráfok, melyeknek nincs négy csúcsból álló húrmentes úttal izomorf feszített részgráfja. Ebből kiindulva számos, tiltott feszített részgráfok alapján meghatározott gráfcsalád klikkszélességét sikerült megállapítani.

A korlátos klikkszélességű gráfok közé tartoznak még a [[Levélhatvány|Sablon:Mvar-adik levélhatványok]] is a Sablon:Mvar korlátos értékeire; ezek a Sablon:Math gráfhatvány Sablon:Mvar levelei által kifeszített részgráfjai. A nem korlátos kitevőjű levélhatványok esetében azonban a klikkszélesség sem korlátos.

Korlátok

Sablon:Harvtxt és Sablon:Harvtxt egyes gráfok klikkszélességével kapcsolatban a következőket igazolták:

• Ha egy gráf klikkszélessége legfeljebb Sablon:Mvar, akkor ez igaz a gráf minden feszített részgráfjára is.
• Egy Sablon:Mvar klikkszélességű gráf komplementerének klikkszélessége legfeljebb Sablon:Math.
• A Sablon:Mvar faszélességű gráfok klikkszélessége legfeljebb Sablon:Math. A korlátban szereplő exponenciális tag szükséges: ténylegesen léteznek olyan gráfok, melyek klikkszélessége exponenciálisan nagyobb a faszélességüknél. Megfordítva, a korlátos klikkszélességű gráfok rendelkezhetnek korlátlan faszélességgel; például az Sablon:Mvar csúcsú teljes gráfok klikkszélessége 2, míg faszélességük Sablon:Math. Azoknak a Sablon:Mvar klikkszélességű gráfoknak viszont, melyek nem tartalmazzák a Sablon:Math teljes páros gráfot részgráfként, legfeljebb Sablon:Math lehet a faszélességük. Így aztán, tetszőleges ritka gráfcsaládra igaz, hogy a korlátos faszélesség ekvivalens a korlátos klikkszélességgel.Sablon:Sfnp
• Egy további gráfparamétert, a rangszélességet (rank-width) mindkét irányból korlátok közé szorít a klikkszélesség: rangszélesség ≤ klikkszélesség ≤ 2^{rangszélesség + 1}.Sablon:Sfnp

Igaz továbbá, hogy ha a Sablon:Mvar gráf klikkszélessége Sablon:Mvar, akkor a Sablon:Math gráfhatvány klikkszélessége legfeljebb Sablon:Math.Sablon:Sfnp Bár mind a klikkszélesség a faszélesség szerinti korlátjában, mind klikkszélesség gráfhatvány szerinti korlátjában exponenciális rés szerepel, ezeknek a korlátok nem szorzódnak össze: ha a Sablon:Mvar gráf faszélessége Sablon:Mvar, akkor Sablon:Math klikkszélessége legfeljebb Sablon:Math, ami a faszélességnek csak egyszeresen exponenciális függvénye.Sablon:Sfnp

Számítási bonyolultság

Sablon:Megoldatlan Számos, általánosabb gráfosztályokon NP-nehéz optimalizálási probléma korlátos klikkszélességű gráfokon dinamikus programozás segítségével hatékonyan megoldható, ha ezen gráfok konstrukciós lépései ismertek.Sablon:SfnpSablon:Sfnp Közelebbről, minden gráftulajdonság, aminek létezése kifejezhető a gráftulajdonságokat logikai műveletekkel, kvantorokkal stb. leíró MSO₁ monadikus másodrendű logika segítségével, a Courcelle-tétel egy változata alapján lineáris idejű algoritmussal eldönthető.Sablon:Sfnp

Polinom időben lehetséges továbbá a korlátos klikkszélességű gráfok optimális gráfszínezését és Hamilton-körét megtalálni, ha a konstrukciós lépések ismertek, de a polinom kitevője a klikkszélességgel növekszik, és a számítási bonyolultságelmélet bizonyítékai arra mutatnak, hogy ettől a függőségtél valószínűleg nem lehet eltekinteni.Sablon:Sfnp A korlátos klikkszélességű gráfok [[χ-korlátos|Sablon:Mvar-korlátosak]], vagyis kromatikus számuk legfeljebb a legnagyobb klikk méretének függvénye lehet.Sablon:Sfnp

A három klikkszélességű gráfok polinom időben felismerhetők, és konstrukciós lépéseik is előállíthatók egy splitfelbontás-alapú algoritmussal.Sablon:Sfnp A nem korlátos klikkszélességű gráfok esetén NP-nehéz a klikkszélesség pontos megállapítása, ahogy a szublineáris additív hibával történő approximációja is.Sablon:Sfnp Ha azonban a klikkszélesség korlátos, egy korlátos szélességű (exponenciálisan nagyobb mint a tényleges klikkszélesség) konstrukciós lépéssorozat polinom időben előállítható. Nyitott egyelőre az a kérdés, hogy a pontos klikkszélesség, vagy akár egy pontosabb approximációja kiszámítható-e rögzített paraméter mellett kezelhető időben, polinom időben kiszámítható-e minden rögzített klikkszélesség-korlát esetén, vagy akár a négy klikkszélességű gráfok felismerhetők-e a polinom időben.Sablon:Sfnp

Faszélességgel való kapcsolata

A korlátos klikkszélességű gráfok elmélete hasonlít a korlátos faszélességű gráfokéhoz, de azoktól eltérően sűrű gráfokkal is foglalkozik. Ha egy gráfcsalád klikkszélessége korlátos, akkor vagy a faszélessége is korlátos, vagy minden teljes páros gráf a család valamely tagjának részgráfja.Sablon:Sfnp A faszélesség és a klikkszélesség az élgráfokon keresztül is összekapcsolódik: egy gráfcsalád pontosan akkor korlátos faszélességű, ha élgráfjaiknak klikkszélessége korlátos.Sablon:Sfnp

Fordítás

• Sablon:Fordítás

Jegyzetek

• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation. Presented in preliminary form in Graph grammars and their application to computer science (Bremen, 1990), Sablon:MR.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.
• Sablon:Citation.