Diffúziós együttható

A diffúziós együttható (D) a molekuláris diffúzió – a részecskék szétterjedése, anyagvándorlása a véletlenszerű hőmozgás, Brown-mozgás következtében - okozta molekulafluxus és az anyag koncentrációgradiense közötti arányossági tényező  Fick I. törvénye alapján. Megadja az egységnyi idő alatt egységnyi felületen átdiffundált anyag mennyiségét, ha a koncentrációesés is egységnyi volt. A diffúziós együttható a részecskék mozgékonyságát, a diffúzió sebességét jellemzi, az Einstein-Smoluchowski-egyenlet szerint a T idő alatt megtett $\lambda$ távolság négyzetátlagából meghatározható:

$D={\lambda }^2/2T$

Ez az egyenlet kapcsolatot teremt a részecskediffúzió mikroszkopikus jellemzői és a diffúzióval kapcsolatos makroszkopikus mennyiségek, pl. a viszkozitás között.

A diffúziós együttható SI-mértékegysége a m²/s (távolság²/idő).

Diffúziós együtthatók gázfázisban

A diffúziós együtthatók gáz fázisban erősen függnek a nyomástól és a hőmérséklettől, két gáz esetén a Chapman-Enskog-elmélet szerint az alábbi egyenlettel írhatók le:

$D_{12}=\frac{3}{8}{\left(\frac{N}{\pi }\frac{M_1+M_2}{2M_1{M}_2}\right)}^{\frac{1}{2}}\frac{(k_{B}T{)}^{\frac{3}{2}}}{p{\sigma }_{12}^2{\mathrm{\Omega }}_{12}^{*}}$

ahol

• 1 és 2 a gázkeverékben található kétféle molekula indexei
• $D_{12}$ – a diffúziós együttható (cm²/s)
• N – az Avogadro-állandó
• M_1,2 – az anyagok moláris tömege
• k_B – a Boltzmann-állandó
• T – az abszolút hőmérséklet (K)
• p – a nyomás (atm)
• ${\sigma }_{12}=\frac{{\sigma }_1+{\sigma }_2}{2}$ - az átlagos ütközési átmérő (Å)
• ${\mathrm{\Omega }}_{12}$– hőmérsékletfüggő ütközési integrál (dimenzió nélküli)

Diffúziós együtthatók folyadékfázisban

A diffúziós együtthatókat folyadék fázisban, gömbszerű részecskéket feltételezve a Stokes-Einstein-egyenlet írja le:

$D=\frac{k_{B}T}{6\pi \eta r_H}$

ahol

• k_B – a Boltzmann-állandó
• T – a hőmérséklet (K)
• η – a viszkozitás (Pas)
• r_H – a diffundáló részecske hidrodinamikai vagy Stokes-sugara (m)

Diffúziós együtthatók szilárd fázisban

A diffúziós együtthatók szilárd fázisban az Arrhenius-egyenlettel írhatók le:

$D=D_0\cdot exp(-\frac{E_a}{RT})$

ahol

• D a diffúziós együttható (m²/s),
• D₀ a maximális diffúziós együttható (végtelen hőmérsékleten; m²/s),
• E_a a diffúzió aktiválási energiája (J/mol),
• T az abszolút hőmérséklet (K),
• R az univerzális gázállandó 8.31446 J/(mol⋅K)

Példák

Gázok 1 atm nyomáson, oldott anyagok az oldatban végtelen hígításban. Jelölések: (s) – szilárd; (l) – folyadék; (g) – gáz; (dis) – oldott.

Diffúziós együttható (gáz)
Oldott anyag - oldószer	Hőmérséklet (°C)	D (cm²/s)	Referencia
Víz (g) – levegő (g)	25	0.282
Oxigén (g) – levegő (g)	25	0.176

Diffúziós együttható (folyadék)
Oldott anyag - oldószer	Hőmérséklet (°C)	D (cm²/s)	Referencia
Aceton (dis) – víz (l)	25	1.16×10−5
Ammónia (dis) – víz (l)	25	1.64×10−5
Benzol (dis) – víz (l)	25	1.02×10−5
Etán (dis) – víz (l)	25	1.20×10−5
Etanol (dis) – víz (l)	25	0.84×10−5
Etén (dis) – víz (l)	25	1.87×10−5
Glükóz (dis) - víz (l)	25	6.70×10−6
Hidrogén (dis) – víz (l)	25	4.50×10−5
Laktóz (dis) - víz (l)	25	4.90×10−6
Metán (dis) – víz (l)	25	1.49×10−5
Metanol (dis) – víz (l)	25	0.84×10−5
Nitrogén (dis) – víz (l)	25	1.88×10−5
Oxigén (dis) – víz (l)	25	2.10×10−5
Propán (dis) – víz (l)	25	0.97×10−5
Szén-dioxid (dis) – víz (l)	25	1.92×10−5
Szén-monoxid (dis) – víz (l)	25	2.03×10−5
Szukróz (dis) - víz (l)	25	5.20×10−6
Víz (l) – aceton (l)	25	4.56×10−5
Víz (l) – etil-alkohol (l)	25	1.24×10−5

Diffúziós együttható (szilárd)
Oldott anyag - oldószer	Hőmérséklet (°C)	D (cm²/s)	Referencia
Hidrogén – vas (s)	10	1.66×10−9
Hidrogén – vas (s)	100	124×10−9
Alumínium – réz (s)	20	1.3×10−30

A diffúziós együttható mérése

A diffúziós együttható mérésére minden olyan fizikai méréstechnika alkalmas, amellyel egy adott tér jól definiált helyén a kérdéses anyag koncentrációjának időfüggése nyomon követhető. A gyakorlatban leginkább alkalmazott technikák a dinamikus fényszórás (DLS – Dynamic Light Scattering) és a diffúziós NMR (PFG – Pulsed Field Gradient, DOSY – Diffusion Spectroscopy). Ezek mellett színes anyagok esetén a fényelnyelés, illetve emisszió mérését alkalmazhatjuk a pillanatnyi koncentráció detektálására, míg töltéssel rendelkező ionok vagy molekulák esetén az elektromosvezetőképesség-mérés módszerét is használhatjuk e célra. NMR spektroszkópia alkalmazásával kétféle diffúziós jelenség is vizsgálható: A relaxációs mérések kiértékelésével a rotációs diffúzió jellemezhető, ami a ps-ns tartományba eső mozgás, a PFG-technikákkal pedig a ms-s-os nagyságrendű transzlációs diffúzió, ez utóbbit jellemezzük a D együtthatóval, és alkalmazzuk molekulaméret meghatározásra. A PFG egy rövid, időzített pulzus, melynek intenzitása egy adott tengely (tipikusan z) mentén változik, és amelyet négy tulajdonság határoz meg: a tengely orientációja, a pulzus erőssége, alakja és időtartama.  A diffúziós mérések legegyszerűbb fajtája a PGSE (Pulsed Gradient Spin Echo, gradiens spin-echo), mely a Hahn-féle spin-echo pulzusszekvencia egy módosított változata. Ebben a mérésben a jelintenzitás (I) csökkenését követjük adott diffúziós paraméterek mellett ($\delta$, $\mathrm{\Delta }$, G). A transzlációs diffúziós együttható meghatározásánál a diffúziós paraméterek közül leginkább a G gradiens erősségét változtatjuk. A jelintenzitás-G lecsengés a Stejskal-Tanner-összefüggés szerint illeszthető, és D értéke meghatározható:

A jelintenzitás lecsengése a gradienserősség függvényében diffúziós NMR mérés esetén

$I=I_{0}exp[-D{\gamma }^2{\delta }^2{G}^2(\mathrm{\Delta }-\frac{\delta }{3})]$

ahol I a jelintenzitás, I₀ a kezdeti jelintenzitás, D a diffúziós együttható.

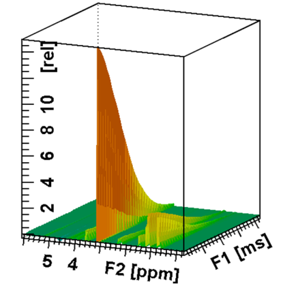
Amennyiben különböző molekulaméretű részecskék vannak az oldatban, a 2D DOSY kiértékelés a célravezetőbb. Az indirekt dimenzió logD értékéből számolható ki a diffúziós együttható, a mérés ilyen fajta értelmezése egy NMR kromatogramra hasonlít.