Végeselemes módszer

Hidraulikus préskeret mechanikai feszültségei

2D VEM megoldás egy magnetostatikai feladatra (a vonalak a mágneses fluxus sűrűségének irányát, a színek az erősségét jelölik)

A fenti probléma megoldásához felvett sík háló (a háló vizsgált hely közelében sűrűbb)

A végeselemes módszer (VEM) numerikus módszer parciális differenciálegyenletek közelítő megoldására. Jellemzően mérnökök használják, a gépészmérnöki és építőmérnöki feladatokkal szorosan összefüggő mechanikai (szilárdságtani és lengéstani) számítások elvégzésére, valamint a villamosmérnöki gyakorlatban mezőszimuláció során is ezt a módszert alkalmazzák.

Lineáris statikus feladat

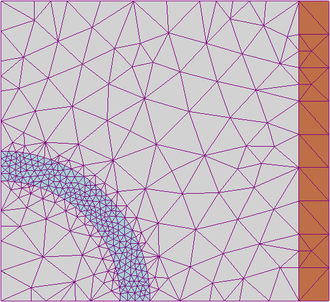
Tipikus példa a végeselemes módszer használatára egy bonyolult alakú statikusan terhelt gépalkatrész feszültségi állapotának és alakváltozásának meghatározása. Ebben az esetben az alkatrészt modellező geometriai testet véges számú elemre bontják: síkbeli problémáknál például háromszögekre vagy négyszögekre, térbeli esetben esetleg hasábokra vagy tetraéderekre. A felosztást úgy célszerű végrehajtani, hogy azokon a részeken, ahol a megoldás szempontjából kritikus lehet az eredmény, ott sűrűbben kisebb méretű, ahol pedig a változások várhatóan kisebb mértékűek lesznek, ott nagyobb méretű elemeket választanak. A modellben az elemek csak sarokpontjaikon (csomópontjaikon) csatlakoznak egymáshoz. A csomópontokon az elemekre ható erők és a csomópontok elmozdulása között a Hooke-törvényt követő anyag esetén lineáris összefüggés van, ezekből összeállítható az elemek merevségi mátrixa. Az elemek merevségi mátrixaiból megszerkeszthető az egész feladat merevségi mátrixa. A feladat ebben a fázisban az alábbi egyenlet megoldására redukálódik:

$\overrightarrow{K}\overrightarrow{u}=\overrightarrow{F},$

ahol

$\overrightarrow{u}$ az m elemű elmozdulásvektor,

$\overrightarrow{F}$ az m elemű terhelésvektor,

$\overrightarrow{K}$ egy m × m elemű szimmetrikus mátrix, a rendszer merevségi mátrixa,

$m=n\cdot k$, a rendszer csomópontjainak (n) és a csomópontok szabadságfokainak (k) szorzata.

Az egyenletrendszer megoldásával kiszámítható az egyes csomópontok elmozdulása, majd az elmozdulásokból a csomóponti erők és a közelítő mechanikai feszültségek. A statikus probléma tehát végső fokon egy lineáris egyenletrendszer megoldását kívánja, amelyre sok jól használható számítógépes módszert dolgoztak ki.

Dinamikai feladatok

A lineáris rendszer csillapítás nélküli lengéseire a következő egyenlet írható fel:

$\overrightarrow{M}\overrightarrow{\ddot{u}}+\overrightarrow{K}\overrightarrow{u}=\overrightarrow{0},$

$\overrightarrow{\ddot{u}}$ a gyorsulásvektor, nem más mint az $\overrightarrow{u}$ elmozdulásvektor idő szerinti második deriváltja,

$\overrightarrow{M}$ szimmetrikus mátrix a tömegmátrix, melynek elemei a rendszer tömegének a csomópontokra redukált diszkrét részeiből épül fel.

$\overrightarrow{0}$ nullvektor, azt fejezi ki, hogy nincs gerjesztés.

A megoldást a következő alakban lehet keresni:

$\overrightarrow{u}=\overrightarrow{h}sin{\alpha }_i$

ahol ${\alpha }_i$ az i-edik sajátérték (sajátfrekvencia),

$\overrightarrow{h}$ pedig az i-ik sajátértékhez tartozó sajátvektor.

Visszahelyettesítve ezeket:

$(-\overrightarrow{M}+\overrightarrow{K})sin{\alpha }_i=\overrightarrow{0}$

Ez a feladat így egy mátrix sajátérték-sajátvektor feladatra vezethető vissza. Gerjesztett lengések és lineáris csillapítás esetén az egyenlet ilyen alakú:

$\overrightarrow{M}\ddot{u}+\overrightarrow{S}\dot{u}+\overrightarrow{K}\overrightarrow{u}=\overrightarrow{f},$

itt

$\overrightarrow{S}$ a csillapítás mátrix,

$\overrightarrow{f}$ pedig a gerjesztőerők vektora

Egyéb feladatok

A végeselemes módszert alkalmazni lehet nemlineáris feladatok megoldására is, mint például nemlineáris anyagtulajdonságok, nagy deformációk kezelésére, szerkezeti stabilitási problémák megoldására (épületszerkezetek stabilitása, kihajlása, külső nyomásnak kitett tartályok horpadása). Használják a VEM programokat hővezetési problémák illetve kombinált hővezetési és szilárdsági problémák megoldására is. Itt a gátolt hőtágulás okozta hőfeszültségek megállapítás az elsődleges cél. Mágneses és elektrosztatikus problémák szintén jól kezelhetők a módszerrel. Újabban gyakran használják a vízépítésben szivárgási és talajmechanikai vizsgálatok elvégzésére is.

Rácsos tartó végeselemes analízisének eredménye. Rúderők (kN) és torzított deformációk

Számítógépes programok

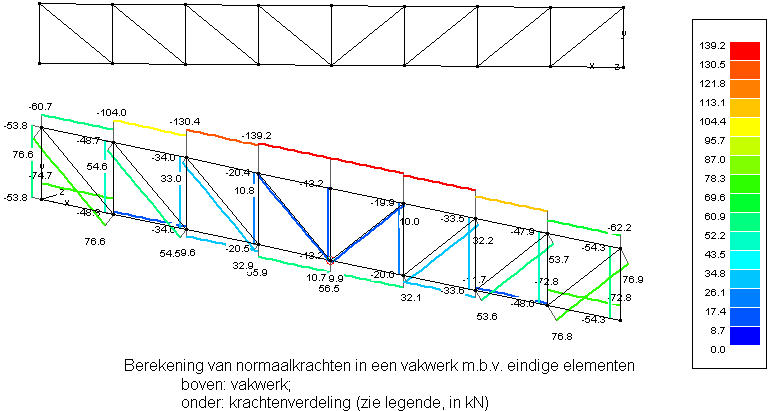
A végeselemes módszer kézi számításokra alkalmatlan, mivel nagyon sok elemi műveletet kellene megoldani hozzá. A mai viszonylag kis teljesítményű személyi számítógépek is alkalmasak azonban, hogy egy sor gyakorlatilag fontos feladat megoldható legyen. A végeselemes módszer alkalmazásánál nemcsak a tulajdonképpeni matematikai feladat (egyenletrendszer megoldása, sajátérték-feladat) megoldása munkaigényes, hanem magának az adatoknak az előkészítése és az eredmények értékelhető alakba hozása is sok időt igényelne. Ezért a korszerű számítógépes programok részét képezi egy preprocesszor és egy posztprocesszor is. A gépalkatrész példa esetén a preprocesszor egy CAD programban elkészített rajzból vagy térbeli modellből kiindulva automatikusan vagy félautomatikusan generálja a végeselemes hálót és ugyancsak segít a terhelések felhasználóbarát megadásában is. A posztprocesszor pedig vagy felrajzolja a torzított léptékű deformált alakot (vagyis a deformációk értékét egy nagyobb számmal megszorozva jól láthatóvá teszi az alakváltozást) vagy szintvonalakkal vagy színezéssel bejelöli a különböző feszültségű tartományokat. Sok új CAD program már tartalmaz egyszerűbb végeselemes modult. Ilyen többek között a Solid Edge, CATIA V5, Autodesk Inventor Professional, SolidWorks, Pro/Engineer.

Ismertebb professzionális kereskedelmi VEM programok:

Aszimmetrikus ütközés okozta feszültségek és deformációk szilárdsági analízise

• ABAQUS
• ADINA
• ALGOR
• Analysis3D
• ANSYS
• CalculiX
• COMSOL
• COSMOS
• FEAP
• Femap
• FEM-Design
• MARC
• NASTRAN
• LS-DYNA
• MESHPARTS
• Simcenter 3D
• SOFiSTiK

Szabad VEM programok:

• Code_Aster
• Elmer
• DUNE
• MoFEM
• Z88

Külső hivatkozások

• Páczelt István, Szabó Tamás, Baksa Attila: A végeselem-módszer alapjai.
• dr. Vörös Gábor: Virtuális munka elve. Véges elem módszer alapjai. BME oktatási segédlet.Sablon:Halott link
• A matematikai modellezés és a végeselem-módszer
• Bojtár Imre – Gáspár Zsolt: A végeselemmódszer matematikai alapjai. BME Tartószerkezetek Mechanikája Tanszék Budapest, 2009

Irodalom

• H.C.Martin, G.F.Carrey: Bevezetés a végeselem-analízisbe. Műszaki könyvkiadó, Budapest, 1976. Sablon:ISBN