Agnesi-féle görbe

Agnesi-féle görbe

Agnesi-féle görbe (ejtsd: Anyeszi) síkgörbe, algebrai görbe, nevét Maria Gaetana Agnesi (1718–1799) olasz nyelvész, matematikus és filozófus után kapta.

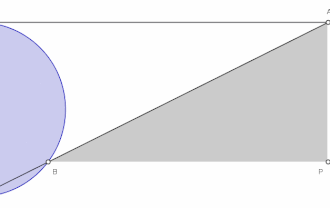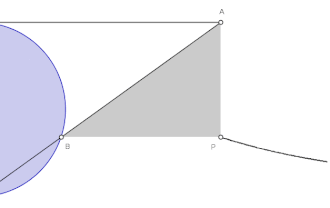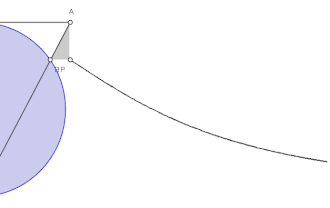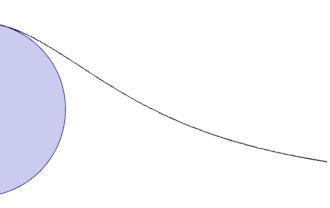
Szerkesztése az ábra jelöléseivel: Jelöljünk ki egy kör kerületén egy O pontot. Húzzuk meg az OA szelőt, az A pont a kör tetszőleges másik pontja. Az M pont az O pont átmérőjén lévő átellenes kör-pont. Az OA szelő N pontban metszi a körhöz az M pontban húzott érintőt. Az N pontban OM-el húzott párhuzamos egyenes és erre az A-ban állított merőleges a P pontban metszi egymást. Az A pont helyének változtatásával ilyen módon megszerkesztett P pontok az Agnesi-féle görbe mértani helyét alkotják.

A görbe aszimptotája a körhöz O pontban húzott érintő, a görbe szimmetrikus az OM egyenesre.

Egyenletei

Az Agnesi-féle görbe szerkesztését mutató animáció

Legyen O pont az origó és M a pozitív y-tengelyen. Legyen a kör sugara a. Ekkor a görbe egyenlete derékszögű koordináta-rendszerben:

$y=\frac{8a^3}{x^2+4a^2}$.

Ha a=1/2, ez az egyenlet ilyen alakra egyszerűsödik:

$y=\frac{1}{x^2+1}.$

Egy paraméteres egyenletrendszere, ha $\vartheta$ az OM és OA egyenesek által bezárt szög az óramutató járása szerint mérve:

$x=2a\mathrm{tg}\vartheta ,y=2a{\cos }^2\vartheta .$

Egy másik paraméteres egyenletrendszer esetén legyen $\phi$ az OA egyenes és az x-tengely által bezárt, az óramutató járásával ellenkező irányban növekvő szög:

$x=2a\mathrm{ctg}\phi ,y=2a{\sin }^2\phi .$

Tulajdonságai

Agnesi-féle görbék a=1, a=2, a=4 és a=8 állandóval.

• Az $M(0,a)$ csúcspontban a görbületi sugár:

$R_M=\frac{a}{2}$

• A görbe inflexiós pontjai:

$B(a\sqrt{3},\frac{3a}{4})$

és

$C(-a\sqrt{3},\frac{3a}{4})$.

Ezekben a pontokban az érintők meredeksége:

$\mathrm{tg}{\alpha }_B=-3\sqrt{3/8}$

és

$\mathrm{tg}{\alpha }_C=3\sqrt{3/8}$

• A görbe és aszimptotája közötti terület négyszerese a származtató kör területének, azaz

$T=4\pi a^2$.

• A görbének, mint meridiángörbének az aszimptota körüli megforgatásával származtatott forgástest térfogata:

$V=4{\pi }^2{a}^3$.

• A görbe súlypontja a $(0,\frac{a}{2})$ pont.

Források

• J. N. Bronstein - K. A. Szemengyajev: Matematikai zsebkönyv. Műszaki könyvkiadó, Budapest, 1987. Sablon:ISBN